Click here to view as pdf.
So, suppose that you were taking an astronomy class as a computer science student. You previously had a physics class and felt fairly confident with what you learned. What is the most likely programming project that you would take on as a final project for your astronomy class? I chose to make a simulator that would demonstrate Newtonian physics or, in other words, an orbital machanics simulator.
Here’s the full script for the people that just want the full thing, and then I’ll step through it and explain the beautiful scotch tape and loose screws (they’re loose by design) that make it work.
from math import pow, sqrt
import time
MAX_SPACE_X = 100
MAX_SPACE_Y = 300
TIME_STEP = 1
class Body:
x = 0.
y = 0.
velocity_x = 0.
velocity_y = 0.
mass = 0
character = ""
is_interstellar = False
def __init__(self, mass, x, y, v_x, v_y, character):
self.mass = mass
self.x = x
self.y = y
self.velocity_x = v_x
self.velocity_y = v_y
self.character = character
def accel_g(M, r):
const_G = pow(10, -4)
return const_G * M / pow(r, 2)
def main():
bodies = [
Body(
4. * pow(10,5),
MAX_SPACE_X / 2,
MAX_SPACE_Y / 2,
0,
0,
# colored character @
"\u001b[33m\u2588\u001b[0m"
),
Body(
1.0 * pow(10,4),
MAX_SPACE_X / 2,
MAX_SPACE_Y / 2 - 10,
1,
0,
"\u001b[32m\u2588\u001b[0m"
),
Body(
1.0 * pow(10,4),
MAX_SPACE_X / 2,
MAX_SPACE_Y / 2 + 20,
-1,
0,
"\u001b[31m\u2588\u001b[0m"
),
Body(
1.0 * pow(10,4),
MAX_SPACE_X / 2,
MAX_SPACE_Y / 2 - 20,
1,
0,
"\u001b[32m\u2588\u001b[0m"
),
Body(
1.0 * pow(10,4),
MAX_SPACE_X / 2,
MAX_SPACE_Y / 2 + 30,
-1,
0,
"\u001b[20m\u2588\u001b[0m"
),
]
while True:
GRID = [[" " for _ in range(MAX_SPACE_X)] for _ in range(MAX_SPACE_Y)]
print("\x1B[2J\x1B[H")
for body in bodies:
if (body.is_interstellar): continue
body_y = int(body.y)
body_x = int(body.x)
GRID[body_y][body_x] = body.character
#GRID[body_y+1][body_x] = body.character
#GRID[body_y-1][body_x] = body.character
#GRID[body_y][body_x+1] = body.character
#GRID[body_y][body_x-1] = body.character
for i in range(MAX_SPACE_X):
for j in range(MAX_SPACE_Y):
print(GRID[j][i], end="")
print()
# calculate accelerations
for i in range(len(bodies)):
body1 = bodies[i]
if (body1.is_interstellar): continue
accel_x = 0
accel_y = 0
for j in range(len(bodies)):
if (i == j): continue
body2 = bodies[j]
if (body2.is_interstellar): continue
dist_x = body1.x - body2.x
dist_y = body1.y - body2.y
distance = sqrt(pow(dist_x, 2) + pow(dist_y, 2))
acceleration = accel_g(body2.mass, distance)
accel_x -= acceleration * dist_x / distance
accel_y -= acceleration * dist_y / distance
#print(f"Accel: {acceleration} x: {accel_x} y: {accel_y}")
body1.velocity_x += accel_x * TIME_STEP
body1.velocity_y += accel_y * TIME_STEP
in_bounds = body1.move()
if (not in_bounds): body1.is_interstellar = True
time.sleep(0.5)
if __name__ == "__main__":
main()
from math import pow, sqrt import time MAX_SPACE_X = 100 MAX_SPACE_Y = 300 TIME_STEP = 1
Starting from the top, I wanted to avoid using pygame or a different visualization tool, and instead create the display using ascii characters. This decision made choosing dependencies very easy, as all I needed were math functions and time. The MAX_SPACE variables define the number of grid cells in each direction. In this case, the X axis runs left to right and the Y axis runs top to bottom, making the top left corner (0, 0). The time step is an arbitrary number that changes how long each simulation frame is. In a “meta” way, it is a leftover from my initial attempt to make this simulator use the metric system. I changed to having no units for simplicity, but I decided to keep the variable so the velocity and position equations would stay the same.
class Body:
x = 0.
y = 0.
velocity_x = 0.
velocity_y = 0.
mass = 0
character = ""
is_interstellar = False
def __init__(self, mass, x, y, v_x, v_y, character):
self.mass = mass
self.x = x
self.y = y
self.velocity_x = v_x
self.velocity_y = v_y
self.character = character
This is the class that represents a single body such as a planet, star, or a moon. It stores important details about the body such as its current position, velocity and mass. The character variable allows me to define an ascii character to represent each body in the display. The is_interstellar variable is just a boolean that is true when a body leaves the simulated area. This keeps the simulation from crashing with an “index out of bounds” error when a body leaves or gets ejected from the simulation area.
def accel_g(M, r):
const_G = pow(10, -4)
return const_G * M / pow(r, 2)
This acceleration function comes from the combination of Newton’s second law and his law of universal gravitation. In mathematical terms, it looks like this:
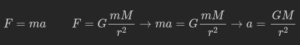
Since there are no units for mass or distance the G constant is just an arbitrary value I found that seems to create a decent result. The important part is the relationship a ∝ M/r^2 that defines how the bodies interract with each other. In laymen’s terms, this means that as bodies get closer together they accelerate faster and larger masses pull things in faster. This fact also comes from Kepler’s laws.
def main():
bodies = [ ... ]
while True:
GRID = [[" " for _ in range(MAX_SPACE_X)] for _ in range(MAX_SPACE_Y)]
print("\x1B[2J\x1B[H")
for body in bodies:
if (body.is_interstellar): continue
body_y = int(body.y)
body_x = int(body.x)
GRID[body_y][body_x] = body.character
#GRID[body_y+1][body_x] = body.character
#GRID[body_y-1][body_x] = body.character
#GRID[body_y][body_x+1] = body.character
#GRID[body_y][body_x-1] = body.character
for i in range(MAX_SPACE_Y):
for j in range(MAX_SPACE_X):
print(GRID[i][j], end="")
print()
The lines that I commented out are for making the bodies appear larger, but it does nothing for the simulation. I removed them after I changed the character for the bodies to a large ascii character.
# calculate accelerations
for i in range(len(bodies)):
body1 = bodies[i]
if (body1.is_interstellar): continue
accel_x = 0
accel_y = 0
for j in range(len(bodies)):
if (i == j): continue
body2 = bodies[j]
if (body2.is_interstellar): continue
dist_x = body1.x - body2.x
dist_y = body1.y - body2.y
distance = sqrt(pow(dist_x, 2) + pow(dist_y, 2))
acceleration = accel_g(body2.mass, distance)
accel_x -= acceleration * dist_x / distance
accel_y -= acceleration * dist_y / distance
#print(f"Accel: {acceleration} x: {accel_x} y: {accel_y}")
body1.velocity_x += accel_x * TIME_STEP
body1.velocity_y += accel_y * TIME_STEP
body1.x += body1.velocity_x * TIME_STEP
body1.y += body1.velocity_y * TIME_STEP
#print(f"x: {body1.x}, y: {body1.y}")
#print(f"v_x: {body1.velocity_x}, v_y: {body1.velocity_y}")
if (body1.x > MAX_SPACE_X or body1.x < 0 or body1.y > MAX_SPACE_Y or body1.y < 0):
body1.is_interstellar = True
time.sleep(0.5)
This is where the magic happens. This calculates the net acceleration on one body that is caused by every other body and then calculates each bodies’ next position. I decided to represent the position, velocity, and acceleration with x and y components, so I used the pythagorean theorem and trigonometry to find the perpendicular components of the acceleration and the complete distance.
This is also where the time step appears, it really does nothing other than preserve the appearence of the equations.
I could have replaced the sleep function with a bit of code that measures the time that the code takes to run and ensures that the total wait time is constant. This would have been cool, but I felt like it was overboard for the breadth of this project, especially considering that the computational requirements for this script are very low.
I really enjoyed this project. It was one of the ideas that is deeply satisfying to make because it is visual. The exitement I felt when watching an ‘o’ orbit around an ‘*’ was phenominal. If I were to expand the project, I would probably add collisions and the Roche limit, which is when a body orbiting a larger body is torn apart by tidal forces. I may also try and recreate this project using SDL so I can create better visuals, if I can avoid creating a memory leak.